Thinking Tokens
Thinking tokens concept (also known as reasoning tokens) enables more intelligence to large models during inference. Until now, the rule to get more intelligent models was only possible through pre-training large model following the “scaling laws”, i.e. adding more training data and computing to pretrain large models.
Now with the concept of “thinking tokens” you can achieve more intelligence with the introduction of an internal model reasoning while doing the next token prediction.
<|startofthought|> and <|endofthought|>
The idea of thinking tokens has been introduced by some authors such as Quiet-STaR: Language Models Can Teach Themselves to Think Before Speaking and latest o1 model from OpenAI. Thinking tokens are named reasoning tokens by OpenAI.
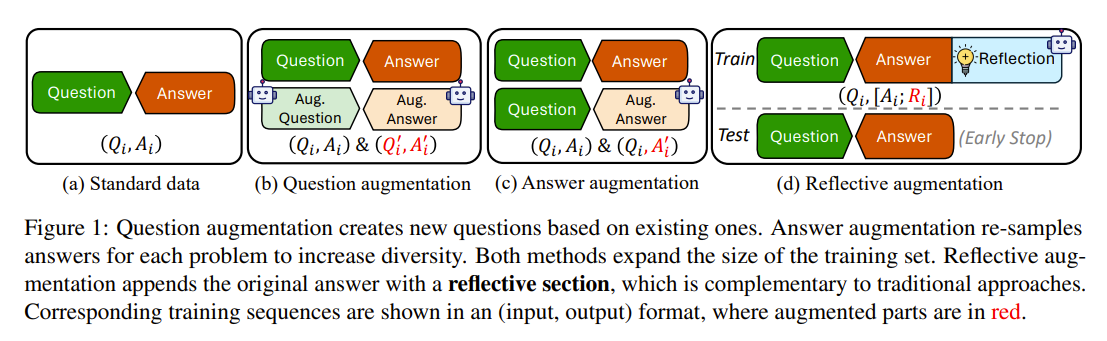
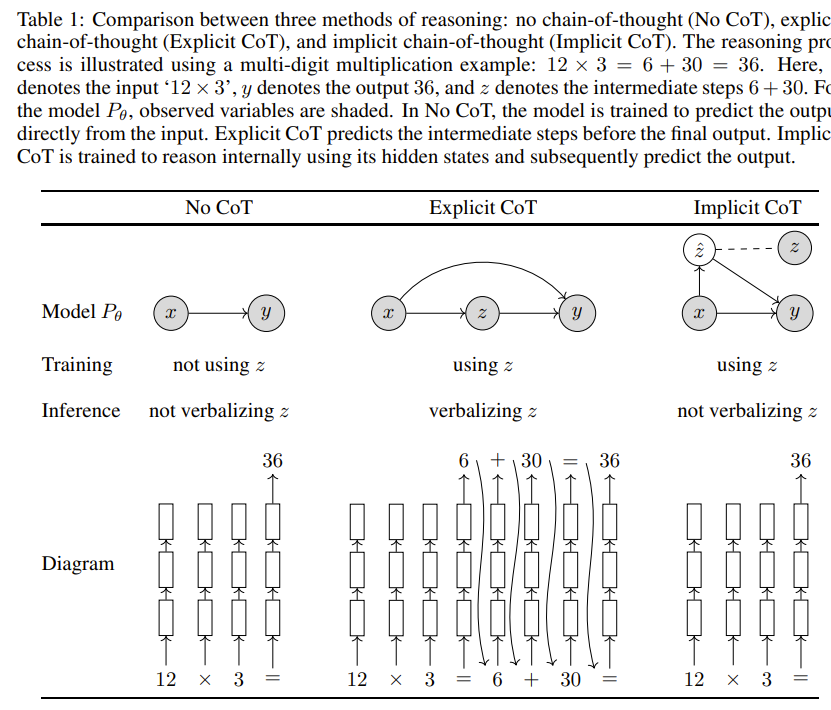
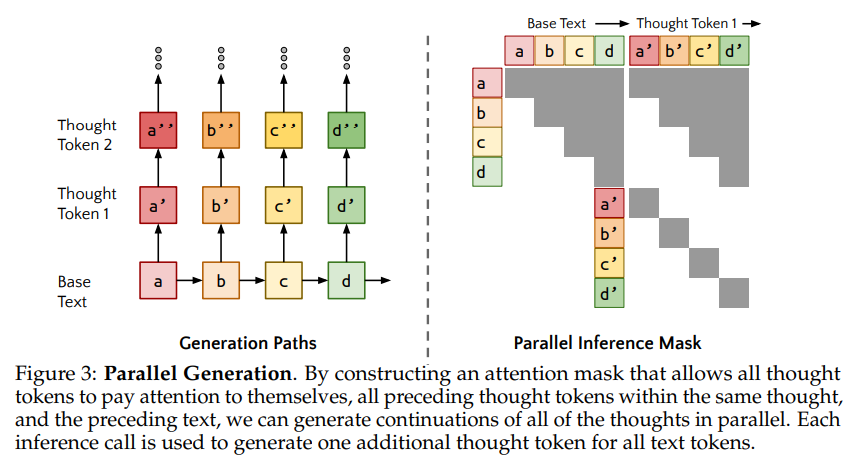
The basic concept is to generate “thinking tokens” at inference time to help model to predict next token. A key challenge is to efficiently generate rationales at each token position in the input sequence. However, as pointed out by simply creating a separate forward pass for each token would be computationally intractable for longer sentences.
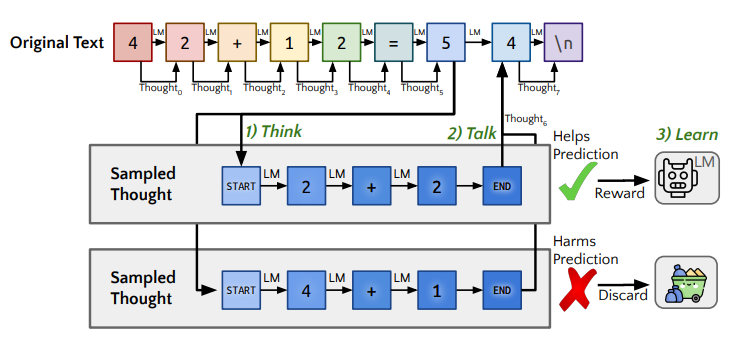
Picture: Quiet-STaR
According to authors, this is done at the inference pass of a language model, when it produces the probability distribution over the next tokens for all input tokens. The solution in Quiet-STaR implements it by caching each forward pass and concatenating a diagonal attention mask to the previous attention mask. Thus each generated token attends to all of the tokens that were used to generate it, as well as itself. But it does not consider the token on the other “counterfactual” paths.
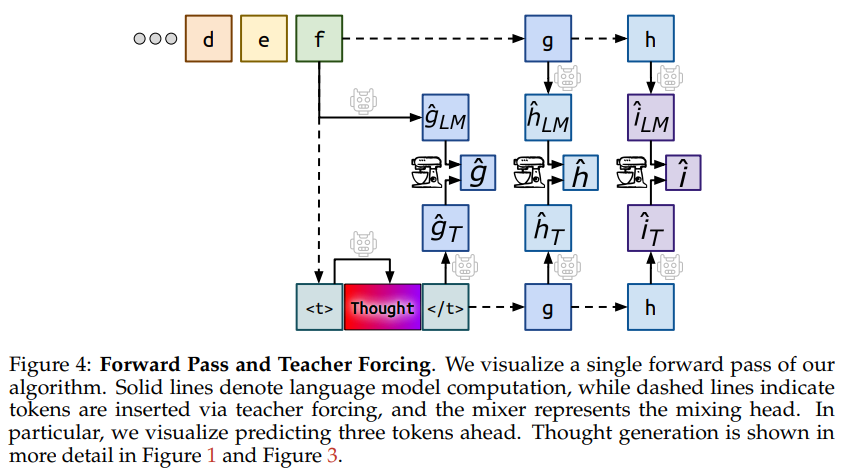
Interestingly, not all tokens requires equal amount of thought .
Interestingly, not all tokens requires equal amount of thought . Thus the thinking token technique does not benefit all tokens equally. For example the sentence “the person is run-”, the “ing” is most probably the token with highest probability and there the additional thinking is unlike to improve a well-trained prediction model.
Thus complex reasoning task such as GSM8K are the ones that would benefit more from the thinking token technique.
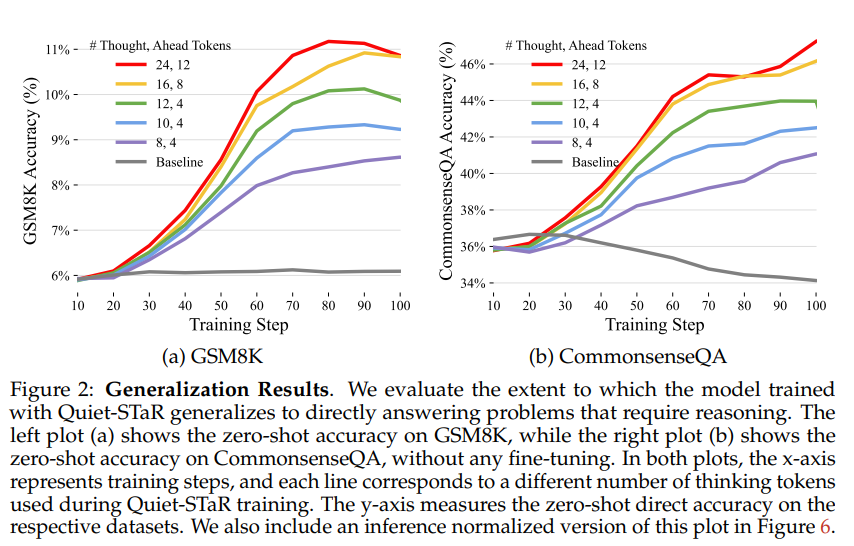
Results:
Amount of thinking tokens increase the accuracy of the models.
As show in figure below, more thinking tokens improve the GSM8K accuracy as the training steps icreases.
Related Work:
Can LLMs learn to think before they speak is a question that several researchers are exploring in order to generate robust internal reasoning processes targeting both training and inference (ref. OpenAI o1-model).
Based on O1 Replication Journey: A Strategic Progress Report by Qin et. al, the following approaches are relevant when trying to answer the question.
Process-level Reward Model: provide fine-grained evaluations of responses from LLMs, specially in mathematical reasoning. The PRMs technique assess model correctness while enhancing post-training quality through search methods such as Monte Carlo Tree Search.
Chain of Thought (CoT) Theory: CoT has advanced reasoning capabilities of LLMs, as intermediate reasoning steps has enhanced LLM performance on tasks such as arithmetic and common sense reasoning. According to researchers, CoT empowers decoder-only models as it enabled inherently serial computations.
Internal Thought: Represents the capability of LLMs to reflect on their reasoning and refinement of its outputs. Quiet-STaR is an approach which following the “Internal Thought” solution by training language models to generate rationales after each token, helping them predict and explain future text more effectively. The work of Zhang et. al (2024) introduces the embedding reflection within each training instance, which encourage the models to review their decisions and consider alternatives paths.
Source: Zhang et. al (2024)
Inference Time Scaling: the idea is that scaling inference time can provide more efficient model performance in comparison the current scaling laws theorem (i.e. increase of number of parameters and training data volume to increase model intelligence). By allowing model more time to process and refine their outputs during inference an alternative scaling dimension appears providing resource efficiency and adaptable computation and consequently reasoning improvements through step-by-step interactive refinement.
Search-to-thought: CoT has gained attention as it improve performance by generating intermediate reasoning steps without search. Implicit Chain-of-Thought Reasoning bypass the need for generating explicit reasoning steps as it can relies on internal hidden states of the model. This is done by using knowledge distilled from a teacher model - training to generate intermediate steps, and allowing student models to solve tasks more efficiently by reasoning vertically through their internal layers (Ref. O1 Replication Journey: A Strategic Progress Report by Qin et. al).
Source: Implicit Chain-of-Thought Reasoning
Self-improvement in LLM: those methods rely on model learning from its outputs without human intervention. Examples are Supervised Fine Tunning (SFT) and preference optimization such as DPO. Here the quality of the model is a function of the external reward system in the form of a reward model, human evaluator or LLM-as-a-Judge prompting. However, finding has suggested that LLM-generated texts often exhibit truncated “tails” - i.e. the distribution of generated output lacks variability found in human-generated content, and can lead to model collapse phenomenon (model converging to a narrower range of behaviors and harming performance) (ref. Shumailov, et. al. (2024)).
Chain of Thought (CoT) Differences
Some differences highlighted by Quiet-STaR authors (here) while comparing thinking tokens to CoT are:
- Different from CoT, model is trained using RL (reinforcement learning) to generate more useful thoughts.
- Rewards model used to generate inner monologues that helps to predict text instead of answers to specific questions - less domain specific.
As pointed by OpenAI here CoT might undermine “thinking tokens”. Thus a best practice are:
- Avoid chain-of-thought prompts: Since these models perform reasoning internally, prompting them to “think step by step” or “explain your reasoning” is unnecessary.
- Limit additional context in retrieval-augmented generation (RAG): When providing additional context or documents, include only the most relevant information to prevent the model from overcomplicating its response.
Latest Developments:
Marco-o1 by MacoPolo Team in Alibaba
Marco-o1 is inspired by OpenAI o1 and leverages different techniques such as:
- CoT (Chain of Thought) fine-tuning
- MCTS (Monte Carlo Tree Search): allow exploration of multiple reasoning paths using confidence scores derived from softmax-applied log probability of the top-k alternative tokens.
- Reasoning Action Strategies: allow to vary granularity of actions within steps and mini-steps to optimize search efficiency and accuracy -
Marco-o1 is a fine tuning of Qwen2-7B-Instruct with a combination of filtered Open-O1 CoT dataset, Marco-o1 CoT dataset and Marco-o1 instruction dataset.
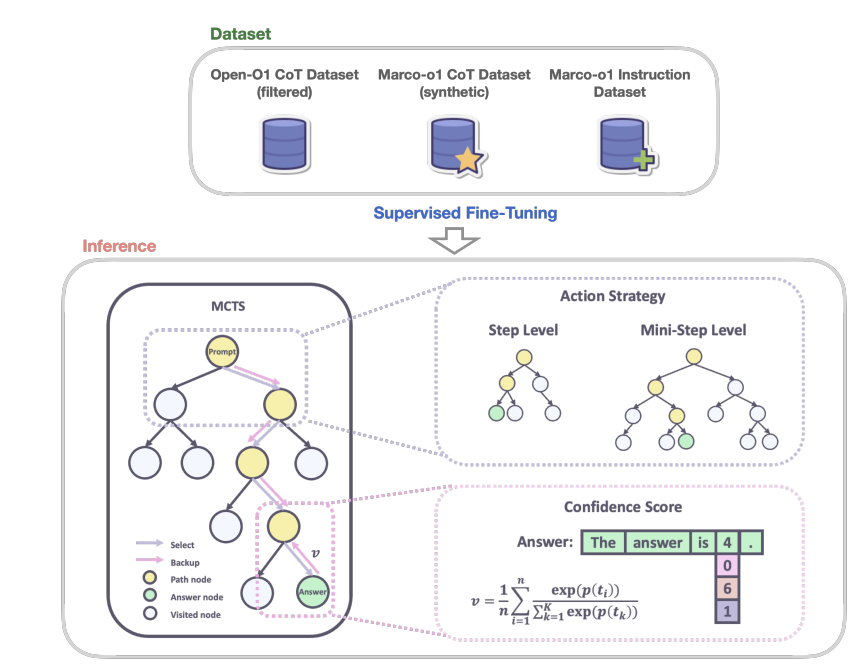
Picture from Marco-o1
**MCTS (Monte Carlo Tree Search):
The Monte Carlo Tree Search enhance the reasoning capability of the model and it is integrated in the model as following:
- Nodes as reasoning states: each node represents a reasoning state of the problem-solving process.
- Actions as LLM outputs: the possible actions from a node are the LLM generated outputs. Each output is a potential step or mini-step in the reasoning chain.
- Rollout and reward calculation: during rollout, the LLM continues the reasoning to a terminal state.
- Guiding MCTS: the reward score R is used to evaluate and select promising paths within the MCTS, guiding the search towards a reliable reasoning chains.
Figure above show v, the average confidence score across all tokens to derive the overall reward score. Where n is the total number of tokens in the rollout sequence. A higher v indicates a more confident and accurate reasoning path.
The confidence score of each state c is calculated by applying a softmax function to its log probability and the log probabilities of the top 5 alternative tokens. Thus ci is the confidence score for the ith token in the rollout. \[ c_{i} = \frac{exp(p(t_{i}))}{\sum_{k=1}^{5}{exp(p(t_{k}))}} \]
Reasoning Action Strategies:
Reasoning action strategies is implemented to allow different levels of granularity in the MCTS search. For example, the concept of mini-steps represents a search space in MCTS in steps composed by smaller units of 64 or 32 tokens. According to authors, it is impractical due to computational resources to execute token level search.
- step as action: model generate complete reasoning steps as actions, where each MCTS node represents an entire thought or action label.
- Mini-step as action: mini-steps of 32 or 64 tokens used as action giving finer granularity to expand the solution space and improve model ability to reasoning tasks by considering mode nuances steps in the search process.
A reflection mechanism “Wait! Maybe I made some mistakes! I need to rethink from scratch.” is added at the end of each though process. This allow the model to self reflect and reevaluate its reasoning steps. As described by authors, the reflection step serves as an internal feedback loop allowing the model to self correct without external intervention.
Experiences with QnQ:
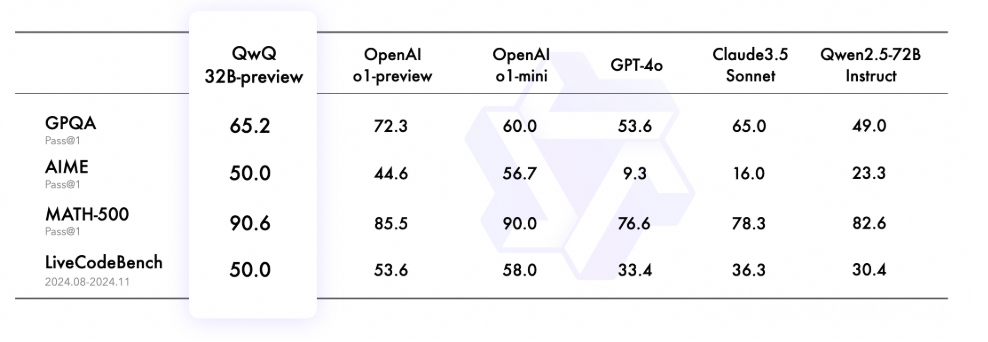
Qwen with Questions (QwQ) from Alibaba is a strong open-source competitor to OpenAI’s GPT-o1 reasoning model. QwQ is available in a 32-billion-parameter preview version with a 32,000-token context.
Based on the blog QwQ: Reflect Deeply on the Boundaries of the Unknown, QnQ has provided important capabilities in challenging mathematical and programming datasets, like:
- GPQA: A Graduate-Level Google-Proof Q&A Benchmark, a challenging benchmark for evaluating scientific problem-solving abilities through grade school level questions.
- AIME: American Invitation Mathematics Evaluation, which tests mathematical problem solving with arithmetic, algebra, counting, geometry, number theory, and probability and other secondary school math topics.
- MATH-500: The 500 test cases of the MATH benchmark, a comprehensive dataset testing mathematical problem-solving.
- LiveCodeBench: A challenging benchmark for evaluating code generation and problem solving abilities in real-world programming scenarios.
Results below show QnQ graduate-level scientific reasoning.
To verify it, I used the QnQ model deployed in HuggingFace here and prompted the same question as in the blog. See section below the “not-so-great” results, which does not follow the results shown by the blog.
Experiments with QnQ 32B preview
Prompt: Please add a pair of parentheses to the incorrect equation: 1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9 = 479, to make the equation true.
Answer: No
Date: 02.12.2024
See the whole though process from QnQ 32B preview here:
Let's tackle this problem step by step. The equation given is:
1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9 = 479
But it's incorrect, and I need to add a pair of parentheses to make it true. Okay, first things first, I should understand what the current value of the left side is without any parentheses.
Let's recall the order of operations: PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). So, multiplication comes before addition.
So, calculating step by step:
2 * 3 = 6
4 * 5 = 20
6 * 7 = 42
8 * 9 = 72
Now, adding them up with the 1:
1 + 6 + 20 + 42 + 72
Let's add these up:
1 + 6 = 7
7 + 20 = 27
27 + 42 = 69
69 + 72 = 141
So, without any parentheses, the left side equals 141, but we need it to equal 479. That's quite a difference, so I definitely need to add parentheses to change the order of operations.
I need to think about where to place the parentheses to get the desired result. Parentheses can group operations together, so whatever is inside the parentheses is calculated first.
Let me consider different possibilities:
Option 1: Parenthesize the entire left side.
(1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
But that's the same as without parentheses, which gives 141, not 479.
Option 2: Group some of the additions and multiplications.
For example, (1 + 2) * 3 + 4 * 5 + 6 * 7 + 8 * 9
Calculate inside the parentheses first:
(1 + 2) = 3
Then, 3 * 3 = 9
Now, add the rest:
9 + 4 * 5 + 6 * 7 + 8 * 9
Following order of operations:
4 * 5 = 20
6 * 7 = 42
8 * 9 = 72
Now, add them up:
9 + 20 + 42 + 72
9 + 20 = 29
29 + 42 = 71
71 + 72 = 143
Still not 479.
Option 3: Try grouping differently.
(1 + 2 * 3) + 4 * 5 + 6 * 7 + 8 * 9
First, calculate inside the parentheses:
1 + 2 * 3
Remember, multiplication comes before addition, so 2 * 3 = 6, then 1 + 6 = 7
Now, the equation becomes:
7 + 4 * 5 + 6 * 7 + 8 * 9
Following order of operations:
4 * 5 = 20
6 * 7 = 42
8 * 9 = 72
Now, add them up:
7 + 20 + 42 + 72
7 + 20 = 27
27 + 42 = 69
69 + 72 = 141
Still not 479.
Option 4: Group more terms inside the parentheses.
(1 + 2 * 3 + 4) * 5 + 6 * 7 + 8 * 9
First, calculate inside the parentheses:
1 + 2 * 3 + 4
Again, multiplication first: 2 * 3 = 6
Then, 1 + 6 + 4 = 11
Now, multiply by 5: 11 * 5 = 55
Then, add the rest:
55 + 6 * 7 + 8 * 9
Following order of operations:
6 * 7 = 42
8 * 9 = 72
Now, add them up:
55 + 42 + 72
55 + 42 = 97
97 + 72 = 169
Still not 479.
Option 5: Try grouping differently.
1 + 2 * (3 + 4) * 5 + 6 * 7 + 8 * 9
First, calculate inside the parentheses:
3 + 4 = 7
Then, 2 * 7 = 14
Now, multiply by 5: 14 * 5 = 70
So, the equation becomes:
1 + 70 + 6 * 7 + 8 * 9
Following order of operations:
6 * 7 = 42
8 * 9 = 72
Now, add them up:
1 + 70 + 42 + 72
1 + 70 = 71
71 + 42 = 113
113 + 72 = 185
Still not 479.
Option 6: Keep trying different groupings.
1 + 2 * 3 + 4 * (5 + 6) * 7 + 8 * 9
First, calculate inside the parentheses:
5 + 6 = 11
Then, 4 * 11 = 44
Then, 44 * 7 = 308
Now, the equation becomes:
1 + 2 * 3 + 308 + 8 * 9
Following order of operations:
2 * 3 = 6
8 * 9 = 72
Now, add them up:
1 + 6 + 308 + 72
1 + 6 = 7
7 + 308 = 315
315 + 72 = 387
Still not 479.
Option 7: Try another grouping.
1 + 2 * 3 + 4 * 5 + 6 * (7 + 8) * 9
First, calculate inside the parentheses:
7 + 8 = 15
Then, 6 * 15 = 90
Then, 90 * 9 = 810
Now, the equation becomes:
1 + 2 * 3 + 4 * 5 + 810
Following order of operations:
2 * 3 = 6
4 * 5 = 20
Now, add them up:
1 + 6 + 20 + 810
1 + 6 = 7
7 + 20 = 27
27 + 810 = 837
Now, 837 is greater than 479, but still not equal to it.
Hmm, maybe I need to think differently. Perhaps grouping the additions together.
Option 8: Group additions first.
(1 + 2) * 3 + 4 * 5 + 6 * 7 + 8 * 9
Wait, I think I already did this in Option 2, which gave 143, not 479.
Option 9: Group differently.
1 + (2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
First, calculate inside the parentheses:
2 * 3 = 6
4 * 5 = 20
6 * 7 = 42
8 * 9 = 72
Now, add them up: 6 + 20 + 42 + 72 = 140
Then, add 1: 1 + 140 = 141
Still not 479.
Option 10: Try nesting parentheses.
1 + 2 * (3 + 4 * (5 + 6) * 7) + 8 * 9
Wait, but the problem says to add only one pair of parentheses. So, I should stick to adding just one pair.
Option 11: Maybe group subtractions or something, but the equation only has additions and multiplications.
Wait, perhaps I need to group in a way that multiplication affects a larger expression.
Option 12: Try (1 + 2 * 3 + 4 * 5 + 6) * 7 + 8 * 9
First, calculate inside the parentheses:
1 + 2 * 3 + 4 * 5 + 6
Following order of operations:
2 * 3 = 6
4 * 5 = 20
So, 1 + 6 + 20 + 6 = 33
Now, multiply by 7: 33 * 7 = 231
Then, add 8 * 9: 231 + 72 = 303
Still not 479.
Option 13: Try (1 + 2 * 3 + 4 * 5 + 6 * 7) + 8 * 9
First, calculate inside the parentheses:
1 + 2 * 3 + 4 * 5 + 6 * 7
Following order of operations:
2 * 3 = 6
4 * 5 = 20
6 * 7 = 42
Now, add them up: 1 + 6 + 20 + 42 = 69
Then, add 8 * 9: 69 + 72 = 141
Still not 479.
Option 14: Maybe group from the other end.
1 + 2 * 3 + 4 * 5 + (6 * 7 + 8 * 9)
First, calculate inside the parentheses:
6 * 7 = 42
8 * 9 = 72
Then, add them: 42 + 72 = 114
Now, the equation becomes:
1 + 2 * 3 + 4 * 5 + 114
Following order of operations:
2 * 3 = 6
4 * 5 = 20
Now, add them up: 1 + 6 + 20 + 114 = 141
Still not 479.
Option 15: Maybe I need to group more terms inside the parentheses.
(1 + 2 * 3 + 4 * 5 + 6 * 7 + 8) * 9
First, calculate inside the parentheses:
1 + 2 * 3 + 4 * 5 + 6 * 7 + 8
Following order of operations:
2 * 3 = 6
4 * 5 = 20
6 * 7 = 42
Now, add them up: 1 + 6 + 20 + 42 + 8 = 77
Then, multiply by 9: 77 * 9 = 693
Now, 693 is larger than 479, but still not equal to it.
Hmm, maybe I need to think outside the box. Perhaps the parentheses need to encompass a subtraction or something, but there are no subtractions in the original equation.
Wait, perhaps I can consider inserting parentheses in a way that changes the order of operations dramatically.
Option 16: (1 + 2) * (3 + 4) * (5 + 6) * (7 + 8) * 9
But that would be more than one pair of parentheses, which violates the problem's condition of adding only one pair.
Option 17: Maybe group additions and multiplications differently.
1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
First, calculate inside the parentheses:
3 + 4 * 5 + 6 * 7 + 8 * 9
Following order of operations:
4 * 5 = 20
6 * 7 = 42
8 * 9 = 72
Now, add them up: 3 + 20 + 42 + 72 = 137
Then, multiply by 2: 2 * 137 = 274
Finally, add 1: 1 + 274 = 275
Still not 479.
Option 18: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8) * 9
Wait, I think I did this in Option 15, which gave 693, not 479.
Option 19: Maybe group differently.
1 + (2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Calculate inside the parentheses:
2 * 3 = 6
4 * 5 = 20
6 * 7 = 42
8 * 9 = 72
Now, add them up: 6 + 20 + 42 + 72 = 140
Then, add 1: 1 + 140 = 141
Still not 479.
Option 20: Maybe consider grouping additions first.
(1 + 2) * 3 + 4 * 5 + 6 * 7 + 8 * 9
Wait, did I not do this in Option 2? Yes, it gave 143.
Option 21: Try a different approach.
Perhaps I need to group in a way that multiplication affects a larger expression to get a bigger number closer to 479.
Option 22: (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 23: Maybe group only part of the expression.
1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
First, calculate inside the parentheses:
3 + 4 * 5 + 6 * 7 + 8 * 9
Following order of operations:
4 * 5 = 20
6 * 7 = 42
8 * 9 = 72
Now, add them up: 3 + 20 + 42 + 72 = 137
Then, multiply by 2: 2 * 137 = 274
Finally, add 1: 1 + 274 = 275
Still not 479.
Option 24: Try grouping fewer terms.
(1 + 2 * 3) + 4 * 5 + 6 * 7 + 8 * 9
Did this in Option 3, which gave 141.
Option 25: Maybe group the last few terms.
1 + 2 * 3 + 4 * 5 + 6 * (7 + 8 * 9)
First, calculate inside the parentheses:
7 + 8 * 9
Following order of operations: 8 * 9 = 72, then 7 + 72 = 79
Now, multiply by 6: 6 * 79 = 474
Then, the equation becomes:
1 + 2 * 3 + 4 * 5 + 474
Following order of operations:
2 * 3 = 6
4 * 5 = 20
Now, add them up: 1 + 6 + 20 + 474 = 501
Now, 501 is closer to 479, but still not it.
Option 26: Maybe adjust the grouping slightly.
1 + 2 * 3 + 4 * (5 + 6 * 7 + 8 * 9)
First, calculate inside the parentheses:
5 + 6 * 7 + 8 * 9
Following order of operations:
6 * 7 = 42
8 * 9 = 72
Now, add them up: 5 + 42 + 72 = 119
Then, multiply by 4: 4 * 119 = 476
Now, the equation becomes:
1 + 2 * 3 + 476
Following order of operations:
2 * 3 = 6
Now, add them up: 1 + 6 + 476 = 483
Close to 479, but still not there.
Option 27: Maybe group differently to get closer.
1 + 2 * 3 + 4 * (5 + 6 * 7 + 8) * 9
First, calculate inside the parentheses:
5 + 6 * 7 + 8
Following order of operations:
6 * 7 = 42
Then, 5 + 42 + 8 = 55
Now, multiply by 4: 4 * 55 = 220
Then, multiply by 9: 220 * 9 = 1980
Now, the equation becomes:
1 + 2 * 3 + 1980
Following order of operations:
2 * 3 = 6
Now, add them up: 1 + 6 + 1980 = 1987
Way beyond 479.
Option 28: Maybe try to subtract somewhere, but there are no subtractions in the original equation.
Wait, perhaps I need to consider that the parentheses might force a subtraction somehow, but that seems unlikely.
Option 29: Let's try to target the multiplication that gives the biggest boost.
Maybe group 6 * (7 + 8 * 9)
First, calculate inside the parentheses:
7 + 8 * 9
Following order of operations: 8 * 9 = 72, then 7 + 72 = 79
Now, multiply by 6: 6 * 79 = 474
Now, the equation becomes:
1 + 2 * 3 + 4 * 5 + 474
Following order of operations:
2 * 3 = 6
4 * 5 = 20
Now, add them up: 1 + 6 + 20 + 474 = 501
Still not 479.
Option 30: Maybe group 4 * (5 + 6 * 7 + 8 * 9)
First, calculate inside the parentheses:
5 + 6 * 7 + 8 * 9
Following order of operations:
6 * 7 = 42
8 * 9 = 72
Now, add them up: 5 + 42 + 72 = 119
Then, multiply by 4: 4 * 119 = 476
Now, the equation becomes:
1 + 2 * 3 + 476
Following order of operations:
2 * 3 = 6
Now, add them up: 1 + 6 + 476 = 483
Still not 479.
Option 31: Maybe adjust the grouping to get closer.
1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
First, calculate inside the parentheses:
3 + 4 * 5 + 6 * 7 + 8 * 9
Following order of operations:
4 * 5 = 20
6 * 7 = 42
8 * 9 = 72
Now, add them up: 3 + 20 + 42 + 72 = 137
Then, multiply by 2: 2 * 137 = 274
Finally, add 1: 1 + 274 = 275
Still not 479.
Option 32: Maybe group larger expressions.
(1 + 2 * 3 + 4 * 5 + 6 * 7 + 8) * 9
Did this in Option 15, which gave 693.
Option 33: Perhaps consider that I need to group in a way that creates a larger multiplication factor.
Option 34: Try (1 + 2 * 3 + 4 * 5 + 6) * (7 + 8 * 9)
But that would be more than one pair of parentheses.
Option 35: Maybe group differently.
1 + (2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Did this in Option 19, which gave 141.
Option 36: Maybe consider that I need to group additions in a specific way to control the multiplication impact.
Option 37: Try (1 + 2 * 3 + 4 * 5 + 6 * 7) + (8 * 9)
But that would be two pairs of parentheses, which is not allowed.
Option 38: Maybe think about the difference between the current sum and the desired sum.
Currently, without any parentheses, the sum is 141, and we need 479.
The difference is 479 - 141 = 338.
Is there a way to add parentheses such that the value increases by 338?
Option 39: Perhaps look for a multiplication factor that can amplify some part of the expression to cover this difference.
Option 40: Maybe consider that multiplying a larger grouped expression could help reach the target.
Option 41: Let's try (1 + 2 * 3 + 4 * 5 + 6) * 7 + 8 * 9
First, calculate inside the parentheses:
1 + 2 * 3 + 4 * 5 + 6
Following order of operations:
2 * 3 = 6
4 * 5 = 20
Now, add them up: 1 + 6 + 20 + 6 = 33
Then, multiply by 7: 33 * 7 = 231
Finally, add 8 * 9: 231 + 72 = 303
Still not 479.
Option 42: Try (1 + 2 * 3 + 4 * 5) + 6 * 7 + 8 * 9
First, calculate inside the parentheses:
1 + 2 * 3 + 4 * 5
Following order of operations:
2 * 3 = 6
4 * 5 = 20
Now, add them up: 1 + 6 + 20 = 27
Then, add 6 * 7: 6 * 7 = 42
27 + 42 = 69
Finally, add 8 * 9: 69 + 72 = 141
Still not 479.
Option 43: Maybe group the additions first.
(1 + 2) * 3 + 4 * 5 + 6 * 7 + 8 * 9
Did this in Option 2, which gave 143.
Option 44: Try (1 + 2 * 3 + 4) * 5 + 6 * 7 + 8 * 9
Did this in Option 4, which gave 169.
Option 45: Maybe group further.
(1 + 2 * 3 + 4 * 5 + 6 * 7) + 8 * 9
Did this in Option 13, which gave 141.
Option 46: Perhaps consider that I need to group in a way that allows for a larger multiplication.
Option 47: Try 1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
Did this in Option 17, which gave 275.
Option 48: Maybe group the last part differently.
1 + 2 * 3 + 4 * (5 + 6 * 7 + 8 * 9)
Did this in Option 26, which gave 483.
Option 49: Perhaps try to group 5 + 6 * 7 + 8 * 9.
Wait, that's part of the previous option.
Option 50: Maybe consider that I need to group in a way that allows for subtraction implicitly.
Wait, but there are no subtractions in the original equation.
Option 51: Maybe think about factoring or some algebraic manipulation.
Option 52: Let's consider the target value, 479, and see how we can reach it.
Option 53: Maybe I need to group in a way that creates a multiplication that results in a number close to 479.
Option 54: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 55: Maybe consider that I need to group the additions and multiplications in a specific order to maximize the value.
Option 56: Try (1 + 2 * 3 + 4 * 5 + 6) * 7 + 8 * 9
Did this in Option 12, which gave 303.
Option 57: Maybe group differently.
1 + (2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Did this in Option 19, which gave 141.
Option 58: Perhaps consider that I need to group the multiplications together.
Option 59: Try 1 + 2 * (3 + 4) * 5 + 6 * 7 + 8 * 9
Did this in Option 5, which gave 185.
Option 60: Maybe group more terms inside the parentheses.
(1 + 2 * 3 + 4 * 5 + 6 * 7 + 8) * 9
Did this in Option 15, which gave 693.
Option 61: Perhaps consider that I need to group in a way that allows for division, but there's no division in the original equation.
Option 62: Maybe I need to think about exponents, but there are no exponents in the original equation.
Option 63: Perhaps consider that the parentheses need to be placed in a way that changes the order of operations drastically, like grouping additions before multiplications.
Option 64: Try (1 + 2) * (3 + 4) * (5 + 6) * (7 + 8) * 9
But that would require multiple pairs of parentheses, which is not allowed.
Option 65: Maybe consider that the parentheses need to be placed around a subtraction, but there are no subtractions.
Option 66: Perhaps think about negative numbers, but there are no negative numbers in the original equation.
Option 67: Maybe consider that I need to group in a way that creates a larger addition before multiplication.
Option 68: Try 1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
Did this in Option 17, which gave 275.
Option 69: Maybe group differently.
1 + (2 * 3 + 4 * 5 + 6 * 7 + 8) * 9
First, calculate inside the parentheses:
2 * 3 + 4 * 5 + 6 * 7 + 8
Following order of operations:
2 * 3 = 6
4 * 5 = 20
6 * 7 = 42
Now, add them up: 6 + 20 + 42 + 8 = 76
Then, multiply by 9: 76 * 9 = 684
Finally, add 1: 1 + 684 = 685
Now, 685 is larger than 479, but still not equal to it.
Option 70: Maybe adjust the grouping.
1 + 2 * (3 + 4 * 5 + 6 * 7 + 8) * 9
First, calculate inside the parentheses:
3 + 4 * 5 + 6 * 7 + 8
Following order of operations:
4 * 5 = 20
6 * 7 = 42
Now, add them up: 3 + 20 + 42 + 8 = 73
Then, multiply by 2: 2 * 73 = 146
Then, multiply by 9: 146 * 9 = 1314
Finally, add 1: 1 + 1314 = 1315
Way beyond 479.
Option 71: Maybe try to group fewer terms.
(1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 72: Perhaps consider that I need to group in a way that allows for a subtraction effect.
Option 73: Maybe think about negative implications, but there are no negatives.
Option 74: Maybe consider that the parentheses need to be placed around the entire expression except for one part.
Option 75: Try 1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
Did this in Option 17, which gave 275.
Option 76: Maybe group differently.
1 + 2 * 3 + 4 * (5 + 6 * 7 + 8 * 9)
Did this in Option 26, which gave 483.
Option 77: Perhaps try to group 5 + 6 * 7 + 8 * 9.
Wait, that's part of the previous option.
Option 78: Maybe consider that I need to group in a way that allows for division, but there's no division in the original equation.
Option 79: Perhaps think about exponents, but there are no exponents.
Option 80: Maybe consider that the problem allows for implied multiplication, but in standard PEMDAS, multiplication and division are at the same level.
Option 81: Maybe think about the distributive property.
Option 82: Perhaps consider factoring part of the expression.
Option 83: Maybe try to factor out a common factor, but there isn't one.
Option 84: Maybe consider that the parentheses need to be placed in a way that creates a larger multiplication factor.
Option 85: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 86: Maybe consider that I need to group the additions and multiplications differently to maximize the value.
Option 87: Perhaps think about the maximum possible value without parentheses and see if it's possible to reach 479.
Without any parentheses, the maximum value would be achieved by performing all multiplications before additions, which is what we did initially, resulting in 141.
But 141 is far from 479, so I need to find a way to increase the value significantly by adding parentheses.
Option 88: Maybe consider that the parentheses need to be placed in a way that allows for a multiplication of a larger sum.
Option 89: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8) * 9
Did this in Option 15, which gave 693.
Option 90: Maybe adjust the grouping to get closer to 479.
Option 91: Perhaps consider that I need to group in a way that allows for subtraction implicitly.
Option 92: Maybe think about negative implications, but there are no negatives.
Option 93: Maybe consider that the problem has no solution, but that seems unlikely since it's given that adding one pair of parentheses can make the equation true.
Option 94: Perhaps I need to group in a way that creates a multiplication that is subtracted or something, but there are no subtractions.
Option 95: Maybe consider that the parentheses need to be placed around a subtraction, but there are no subtractions.
Option 96: Perhaps think about the order of operations in a different way.
Option 97: Maybe consider that the multiplication needs to be grouped in a specific way to maximize the value.
Option 98: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 99: Maybe consider that I need to group the multiplications together.
Option 100: Perhaps think about factoring out a multiplication.
Wait, perhaps I can factor out a common multiplication factor, but there isn't one.
Option 101: Maybe consider that the parentheses need to be placed around the additions.
Option 102: Try 1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
Did this in Option 17, which gave 275.
Option 103: Maybe group differently.
1 + 2 * 3 + 4 * (5 + 6 * 7 + 8 * 9)
Did this in Option 26, which gave 483.
Option 104: Perhaps consider that I need to group in a way that allows for a multiplication of a sum that includes multiple terms.
Option 105: Maybe think about the difference between the current sum and the target, which is 479 - 141 = 338.
Is there a way to add parentheses such that the value increases by 338?
Option 106: Maybe consider that multiplying a group of terms by another term could amplify the difference needed.
Option 107: Perhaps think about the factor by which 141 needs to be increased to reach 479.
479 / 141 is approximately 3.4, but since we're dealing with integers, that doesn't directly help.
Option 108: Maybe consider that I need to group terms to create a multiplication that results in a number close to 479.
Option 109: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8) * 9
Did this in Option 15, which gave 693.
Option 110: Maybe adjust the grouping to reduce the final value.
Option 111: Perhaps consider that I need to group in a way that allows for division, but there's no division in the original equation.
Option 112: Maybe think about exponents, but there are no exponents.
Option 113: Perhaps consider that the problem has no solution, but that seems unlikely.
Option 114: Maybe think about the properties of the operations involved.
Option 115: Perhaps consider that addition is commutative and associative, but multiplication is not.
Option 116: Maybe think about distributing multiplication over addition.
Option 117: Perhaps consider factoring out a common factor, but there isn't one.
Option 118: Maybe consider that the parentheses need to be placed around a specific group of terms to achieve the desired result.
Option 119: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 120: Maybe consider that I need to group the multiplications together.
Option 121: Perhaps think about the distributive property to combine terms.
Option 122: Maybe consider that the parentheses need to be placed around the additions to maximize their impact.
Option 123: Try 1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
Did this in Option 17, which gave 275.
Option 124: Maybe group differently.
1 + 2 * 3 + 4 * (5 + 6 * 7 + 8 * 9)
Did this in Option 26, which gave 483.
Option 125: Perhaps consider that I need to group in a way that allows for a multiplication of a larger sum.
Option 126: Maybe think about the target value, 479, and see how it relates to the current sum, 141.
Option 127: Maybe consider that I need to add another multiplication factor to reach 479.
Option 128: Perhaps think about the difference, 338, and see if there's a way to incorporate that into the equation.
Option 129: Maybe consider that the parentheses need to be placed around a subtraction, but there are no subtractions.
Option 130: Perhaps think about negative implications, but there are no negatives.
Option 131: Maybe consider that the problem has no solution, but that seems unlikely.
Option 132: Perhaps think about the properties of the operations involved.
Option 133: Maybe consider that addition and multiplication have different precedence and see if grouping can exploit that.
Option 134: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 135: Maybe consider that I need to group the additions and multiplications in a specific order to maximize the value.
Option 136: Perhaps think about factoring or some algebraic manipulation.
Option 137: Maybe consider that the problem requires a creative approach beyond standard arithmetic.
Option 138: Perhaps think about the equation in terms of variables and see if that helps.
Option 139: Maybe consider that the parentheses need to be placed in a way that creates a multiplication that is then added to other terms to reach 479.
Option 140: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 141: Maybe consider that the problem has no solution, but that seems unlikely.
Option 142: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 143: Maybe consider that the maximum value is 693, which is still less than 479, but wait, in Option 15, it was 693, which is larger than 479.
Wait, in Option 15, (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8) * 9 = 77 * 9 = 693
But 693 is larger than 479, but perhaps I can adjust the grouping to get closer.
Option 144: Maybe try to exclude one multiplication from the grouping.
Option 145: Try (1 + 2 * 3 + 4 * 5 + 6) * 7 + 8 * 9
Did this in Option 12, which gave 303.
Option 146: Maybe adjust the grouping to include fewer terms in the parentheses.
Option 147: Perhaps think about the impact of each grouping on the total sum.
Option 148: Maybe consider that I need to group in a way that allows for a multiplication that is then added to reach 479.
Option 149: Perhaps think about the difference between 693 and 479, which is 693 - 479 = 214.
Is there a way to adjust the grouping to reduce the total by 214?
Option 150: Maybe consider that excluding certain terms from the multiplication could reduce the total.
Option 151: Perhaps try (1 + 2 * 3 + 4 * 5 + 6 * 7) + 8 * 9
Did this in Option 13, which gave 141.
Option 152: Maybe consider that including more terms in the multiplication increases the total beyond 479, so perhaps grouping fewer terms would help.
Option 153: Perhaps think about grouping only part of the expression.
Option 154: Try 1 + 2 * (3 + 4 * 5 + 6 * 7 + 8 * 9)
Did this in Option 17, which gave 275.
Option 155: Maybe consider that grouping fewer terms results in a lower total.
Option 156: Perhaps think about the balance between additions and multiplications.
Option 157: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 158: Perhaps think about the target value, 479, and see what combinations of the terms can reach it.
Option 159: Maybe consider that the problem requires a specific grouping that isn't immediately obvious.
Option 160: Perhaps think about the equation in terms of variables and see if that helps.
Option 161: Maybe consider that the parentheses need to be placed around a specific group of terms to achieve the desired result.
Option 162: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 163: Maybe consider that the problem has no solution, but that seems unlikely.
Option 164: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 165: Maybe consider that the maximum value is 693, which is larger than 479, but I need to find a way to adjust the grouping to get exactly 479.
Option 166: Maybe think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to subtract 214.
Option 167: But there are no subtractions in the original equation, so that seems impossible.
Option 168: Perhaps consider that the parentheses need to be placed in a way that creates a multiplication that is then added to other terms to reach 479.
Option 169: Maybe think about the factors involved.
Option 170: Perhaps consider that 479 is a prime number, which might influence the grouping.
Option 171: Maybe consider that the parentheses need to be placed around a multiplication that results in 479 minus the sum of the remaining terms.
Option 172: For example, if the remaining terms add up to X, then the multiplication inside the parentheses should be equal to 479 - X.
Option 173: But without knowing X, that might not help directly.
Option 174: Maybe consider specific groupings again.
Option 175: Try (1 + 2 * 3 + 4 * 5 + 6) * 7 + 8 * 9
Did this in Option 12, which gave 303.
Option 176: Maybe adjust the grouping to include more terms in the multiplication.
Option 177: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8) * 9
Did this in Option 15, which gave 693.
Option 178: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 179: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to subtract 214.
Option 180: But again, there are no subtractions in the original equation.
Option 181: Maybe consider that the problem has no solution, but that seems unlikely.
Option 182: Perhaps think about the properties of the operations involved.
Option 183: Maybe consider that addition and multiplication are both associative and commutative, but parentheses can change the order of operations.
Option 184: Perhaps consider that the parentheses need to be placed around a specific group of terms to achieve the desired result.
Option 185: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 186: Maybe consider that the problem has no solution, but that seems unlikely.
Option 187: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 188: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 189: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 190: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 191: But without subtraction, that seems difficult.
Option 192: Maybe consider that the problem has no solution, but that seems unlikely.
Option 193: Perhaps think about the properties of the numbers involved.
Option 194: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 195: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 196: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 197: But without knowing M or S, that might not help directly.
Option 198: Maybe consider specific groupings again.
Option 199: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 200: Maybe consider that the problem has no solution, but that seems unlikely.
Option 201: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 202: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 203: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 204: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 205: But without subtraction, that seems difficult.
Option 206: Maybe consider that the problem has no solution, but that seems unlikely.
Option 207: Perhaps think about the properties of the numbers involved.
Option 208: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 209: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 210: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 211: But without knowing M or S, that might not help directly.
Option 212: Maybe consider specific groupings again.
Option 213: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 214: Maybe consider that the problem has no solution, but that seems unlikely.
Option 215: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 216: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 217: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 218: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 219: But without subtraction, that seems difficult.
Option 220: Maybe consider that the problem has no solution, but that seems unlikely.
Option 221: Perhaps think about the properties of the numbers involved.
Option 222: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 223: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 224: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 225: But without knowing M or S, that might not help directly.
Option 226: Maybe consider specific groupings again.
Option 227: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 228: Maybe consider that the problem has no solution, but that seems unlikely.
Option 229: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 230: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 231: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 232: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 233: But without subtraction, that seems difficult.
Option 234: Maybe consider that the problem has no solution, but that seems unlikely.
Option 235: Perhaps think about the properties of the numbers involved.
Option 236: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 237: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 238: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 239: But without knowing M or S, that might not help directly.
Option 240: Maybe consider specific groupings again.
Option 241: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 242: Maybe consider that the problem has no solution, but that seems unlikely.
Option 243: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 244: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 245: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 246: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 247: But without subtraction, that seems difficult.
Option 248: Maybe consider that the problem has no solution, but that seems unlikely.
Option 249: Perhaps think about the properties of the numbers involved.
Option 250: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 251: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 252: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 253: But without knowing M or S, that might not help directly.
Option 254: Maybe consider specific groupings again.
Option 255: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 256: Maybe consider that the problem has no solution, but that seems unlikely.
Option 257: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 258: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 259: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 260: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 261: But without subtraction, that seems difficult.
Option 262: Maybe consider that the problem has no solution, but that seems unlikely.
Option 263: Perhaps think about the properties of the numbers involved.
Option 264: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 265: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 266: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 267: But without knowing M or S, that might not help directly.
Option 268: Maybe consider specific groupings again.
Option 269: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 270: Maybe consider that the problem has no solution, but that seems unlikely.
Option 271: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 272: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 273: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 274: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 275: But without subtraction, that seems difficult.
Option 276: Maybe consider that the problem has no solution, but that seems unlikely.
Option 277: Perhaps think about the properties of the numbers involved.
Option 278: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 279: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 280: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 281: But without knowing M or S, that might not help directly.
Option 282: Maybe consider specific groupings again.
Option 283: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 284: Maybe consider that the problem has no solution, but that seems unlikely.
Option 285: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 286: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 287: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 288: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 289: But without subtraction, that seems difficult.
Option 290: Maybe consider that the problem has no solution, but that seems unlikely.
Option 291: Perhaps think about the properties of the numbers involved.
Option 292: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 293: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 294: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 295: But without knowing M or S, that might not help directly.
Option 296: Maybe consider specific groupings again.
Option 297: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 298: Maybe consider that the problem has no solution, but that seems unlikely.
Option 299: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 300: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 301: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 302: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 303: But without subtraction, that seems difficult.
Option 304: Maybe consider that the problem has no solution, but that seems unlikely.
Option 305: Perhaps think about the properties of the numbers involved.
Option 306: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 307: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 308: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 309: But without knowing M or S, that might not help directly.
Option 310: Maybe consider specific groupings again.
Option 311: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 312: Maybe consider that the problem has no solution, but that seems unlikely.
Option 313: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 314: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 315: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 316: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 317: But without subtraction, that seems difficult.
Option 318: Maybe consider that the problem has no solution, but that seems unlikely.
Option 319: Perhaps think about the properties of the numbers involved.
Option 320: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 321: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 322: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 323: But without knowing M or S, that might not help directly.
Option 324: Maybe consider specific groupings again.
Option 325: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 326: Maybe consider that the problem has no solution, but that seems unlikely.
Option 327: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 328: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 329: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 330: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 331: But without subtraction, that seems difficult.
Option 332: Maybe consider that the problem has no solution, but that seems unlikely.
Option 333: Perhaps think about the properties of the numbers involved.
Option 334: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 335: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 336: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 337: But without knowing M or S, that might not help directly.
Option 338: Maybe consider specific groupings again.
Option 339: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 340: Maybe consider that the problem has no solution, but that seems unlikely.
Option 341: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 342: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 343: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 344: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 345: But without subtraction, that seems difficult.
Option 346: Maybe consider that the problem has no solution, but that seems unlikely.
Option 347: Perhaps think about the properties of the numbers involved.
Option 348: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 349: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 350: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 351: But without knowing M or S, that might not help directly.
Option 352: Maybe consider specific groupings again.
Option 353: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 354: Maybe consider that the problem has no solution, but that seems unlikely.
Option 355: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 356: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 357: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 358: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 359: But without subtraction, that seems difficult.
Option 360: Maybe consider that the problem has no solution, but that seems unlikely.
Option 361: Perhaps think about the properties of the numbers involved.
Option 362: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 363: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 364: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 365: But without knowing M or S, that might not help directly.
Option 366: Maybe consider specific groupings again.
Option 367: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 368: Maybe consider that the problem has no solution, but that seems unlikely.
Option 369: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 370: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 371: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 372: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 373: But without subtraction, that seems difficult.
Option 374: Maybe consider that the problem has no solution, but that seems unlikely.
Option 375: Perhaps think about the properties of the numbers involved.
Option 376: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 377: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 378: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 379: But without knowing M or S, that might not help directly.
Option 380: Maybe consider specific groupings again.
Option 381: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 382: Maybe consider that the problem has no solution, but that seems unlikely.
Option 383: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 384: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 385: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 386: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 387: But without subtraction, that seems difficult.
Option 388: Maybe consider that the problem has no solution, but that seems unlikely.
Option 389: Perhaps think about the properties of the numbers involved.
Option 390: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 391: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 392: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 393: But without knowing M or S, that might not help directly.
Option 394: Maybe consider specific groupings again.
Option 395: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 396: Maybe consider that the problem has no solution, but that seems unlikely.
Option 397: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 398: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 399: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 400: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 401: But without subtraction, that seems difficult.
Option 402: Maybe consider that the problem has no solution, but that seems unlikely.
Option 403: Perhaps think about the properties of the numbers involved.
Option 404: Maybe consider that 479 is a prime number, which might influence the grouping.
Option 405: Maybe consider that the multiplication needs to result in a number that, when added to the remaining terms, equals 479.
Option 406: For example, if the multiplication inside the parentheses is M, and the sum of the remaining terms is S, then M + S = 479.
Option 407: But without knowing M or S, that might not help directly.
Option 408: Maybe consider specific groupings again.
Option 409: Try (1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9)
Wait, that's the same as without parentheses, which is 141.
Option 410: Maybe consider that the problem has no solution, but that seems unlikely.
Option 411: Perhaps think about the maximum possible value achievable with one pair of parentheses.
Option 412: Maybe consider that 693 is the maximum value I can get with one pair of parentheses, which is still larger than 479.
Option 413: Maybe consider that I need to group in a way that allows for a multiplication that is then added to other terms to reach 479.
Option 414: Perhaps think about the difference between 693 and 479, which is 214, and see if there's a way to adjust the grouping to reduce the total by 214.
Option 415: But without subtraction, that seems difficult.
Option 416: Maybe consider that the problem has no solution, but that seems unlikely.
Option
References:
Quiet-STaR: Language Models Can Teach Themselves to Think Before Speaking
O1 Replication Journey: A Strategic Progress Report by Qin et. al
State of AI Report 2024 by Nathan Benaich
Model: Marco-o1: Towards Open Reasoning Models for Open-Ended Solutions
Model: Open O1: A Model Matching Proprietary Power with Open-Source Innovation
Dataset: Open O1 SFT